The reflective properties of conic sections and their applications.

The reflective property of a parabola
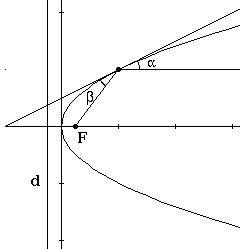
Let P be a point on a parabola. Let l be the line through P and the focus. Let m be a line through P perpendicular to the directrix of the parabola. Let t be the tangent line of P. Then the angle between l and t and the angle between m and t are equal.

The application of reflective property of a parabola
Parabaloid is a surface that is formed by revolving a parabola about its axis. One of the applications of the reflective properties of a parabola is a parabolic mirror. It is a mirror in a shape of a parabaloid. It is widely used in reflecting telescopes: when it receives light rays from a distant point source (e.g. star), which are parallel to the axis of the parabola, it reflects them to form a sharp image at the focus. On the other hand, when the point source is at the focus, the reflected light rays will be parallel to each other. This is used in an automobile headlight to form a beam of light. It can also be used in radar antenna.






The reflective property of an ellipse and a hyperbola :
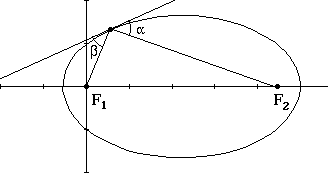
Let P be a point on an ellipse ( or hyperbola). Let l be the line through P and one focus. Let m be a line through P and another focus. Let t be the tangent line of P. Then the angle between l and t and the angle between m and t are equal.

The application of reflective property of an ellipse and a hyperbola:
Ellipsoid is a surface that is formed by revolving an ellipse about its major axis. Let's suppose that we have a mirror in the form of an ellipsoid, which inner surface is silvered. Then a light ray emitted from one focus will be reflected to another focus. Since we could treat sound waves as rays, this is also true for sound. Therefore, in rooms where a ceiling is elliptical, two people, standing at the two foci will hear each other very clearly, This has been called the whispering gallery effect and has been used in the design of special rooms. A good example of this is St. Paul's Cathedral. The reflective property of hyperbola is used in telescopic lenses.