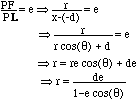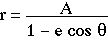Standard Polar Equations for Conic Sections
We have shown that each conic section (except a circle) has the following property, which we will refer to as the "Focus-Directrix" property:
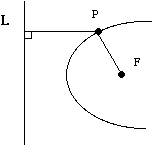
For each conic section which is not a circle, there is a line L, and a point F not on L, and a real number e, for which each point P on the conic sections satisfies the relation PF/P L = e.
We call F a focus, L a directrix, and e the eccentricity of the conic section.
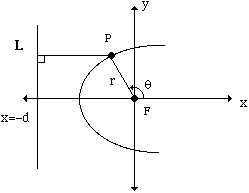
If we put the focus F at the origin, and directrix L at x = - d, then we can derive a polar equation for the conic section.
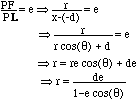 The graph of the conic section is only a single point if e = 0, so it is convenient to replace de with a non-zero constant A in the numerator. Now every conic section, including circles, can be represented indard form by the polar equation
The graph of the conic section is only a single point if e = 0, so it is convenient to replace de with a non-zero constant A in the numerator. Now every conic section, including circles, can be represented indard form by the polar equation
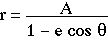 Where
Where
- e is the eccentricity, and
- whenever e is nonzero, d = A/e is the distance to the directrix.
Questions:
- Graph conic sections for many different values of e. Describe the kinds of curves you get with different values of e.
- What picture and formula do you get for conic sections if you choose the line y = -d for the directrix instead of the line x = -d? What if you choose x = d? How about y = d?
- The point on a conic section corresponding to t = π is called a vertex, V. Find a formula for the distances VF and VL in terms of d and e.
- When e is not 1, there is a second vertex W, corresponding to t = 0. Find a formula for the distances WF and VW in terms of d and e.
- Find the distance from the focus F to the point on a conic section corresponding to t = π/2 in terms of d and e.
Last Update: September 19, 2002
Ronald K. Smith
Graceland University
Lamoni, IA 50140
rsmith@graceland.edu